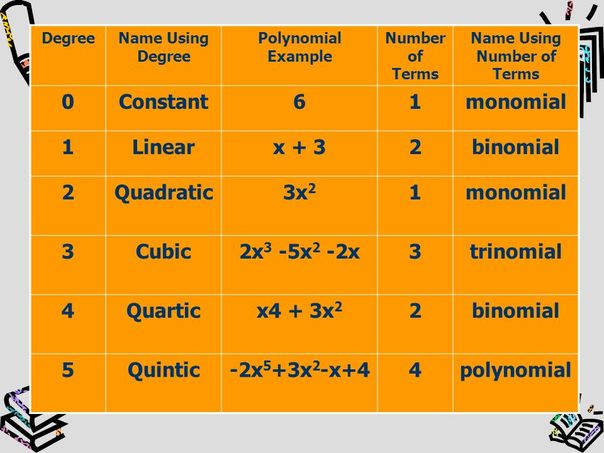
3x2 X 4 Polynomial

Polynomials Exercise 2 3 Class 10 Breath Math

Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver

How To Solve X In X 1 4 X 1 4 16 Mathematics Stack Exchange

Find The Zeros Of The Quadratic Polynomial 3xsquare X 4 And Verify The Relationship Between The Brainly In

Sec 4 4

Topic 11 Polynomials
The correct answer is that 3x ²11x8 will be a polynomial Explanation When we subtract polynomials, we combine like terms 3x ² is the only x ² term we have We have 6x and subtract 5x from it;.

3x2 x 4 polynomial. Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi (Product) Notation Induction Logical Sets Pre Calculus. Question Question 1 Evaluate The Polynomial Function Of P(x) = 3x2 X 4 And Find P(3) P(3) = 7 P(3) = 24 P(3) = 26 P(3) = 28 05 Points Question 2 A Wooden Plank Is (2x2 5x 9) Meters Long If A Piece (x2 5) Meters In Length Is Cut Off The Plank, How Long Is The Remaining Piece?. Click here👆to get an answer to your question ️ Find all zeroes of the polynomial 2x^4 9x^3 5x^2 3x 1 if two of its zeroes are 2 √(3) and 2 √(3).
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor. Polynomial in Ascending Order Calculator The polynomial is said to be in ascending order when the powers series are ordered in small to bigSo, explore more about polynomials in ascending order by referring to their entire article Also, utilize our free online tool ie, Polynomial in Ascending Order Calculator & get the result for any type of complex polynomial equations in ascending order. Multiplying Polynomials – Explanation & Examples Many students will find the lesson of multiplication of polynomials a bit challenging and boring Thanks to this article, because it will help you to understand how different types of polynomials are multiplied Before jumping into multiplying polynomials, let’s recall what monomials, binomials and polynomials are A monomial is.
If x 4 is a factor then x = 4 is a root f(4) = 4^3 2 * 4^2 5 * 4 1 = 64 32 1 = 53 since f(4) is not zero then 4 is not a root of the f(x) Also x 4 is not a factor. For polynomials in two or more variables, the degree of a term is the sum of the exponents of the variables in the term;. Which polynomial represents (3x^2x4)(2x5)?.
Polynomial Function Root or Multipli Zero city Characteris tics of multiplicity Odd or Even Behavior of the graph relative to x axis at this root Crosses or is Tangent to 1 f(x) = x²(x 2)(x 1)2 2 y = (x 1)2(x 1)(x3) E Complete the table Polynomial Function Sketch Give the following 1 y=x* OS Degree No of turning pts. You can also divide polynomials (but the result may not be a polynomial) Degree The degree of a polynomial with only one variable is the largest exponent of that variable. It is the same but just instead of getting 0 you get a polynomial in the last step Divide # 3x^3 – 5x^2 10x – 3 # by # 3x 1# in this case you get a polynomial seven which can be writtten in algebraic terms as #7x^0# so this can be proved using the division algoritm.
Polynomial 3x2 x 4 can be used to find the remaining roots 3x^2 x 4 can be solved by completing the square Divide each term by 3 x^2 1/3x 4/3 = 0 Add 4/3 to both sides x^2 1/3x = 4/3 Double the xcoefficient, square it, and add it to both sides. Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor.
Solving 3x2x4 = 0 directly Earlier we factored this polynomial by splitting the middle term let us now solve the equation by Completing The Square and by using the Quadratic Formula Parabola, Finding the Vertex 41 Find the Vertex of y = 3x2x4. X – 4 ii 5x 5 4x 4 – 3x 3 2x 2 2;. The degree (sometimes called the total degree) of the polynomial is again the maximum of the degrees of all terms in the polynomial For example, the polynomial x 2 y 2 3x 3 4y has degree 4, the same degree as the term x.
Online calculation with the function expand_and_simplify according to the expand_and_simplify((3x1)(2x4)). For a Multivariable Polynomial If we take a polynomial expression with two variables, say x and y \(x^3 3x^2y^4 4y^2 6\) We follow the above steps, with an additional step of adding the powers of different variables in the given terms Here, the degree of the polynomial is 6. Rational Roots Test The Rational Roots Test (also known as Rational Zeros Theorem) allows us to find all possible rational roots of a polynomial Suppose a is root of the polynomial P\left( x \right) that means P\left( a \right) = 0In other words, if we substitute a into the polynomial P\left( x \right) and get zero, 0, it means that the input value is a root of the function.
The largest power of x in the original polynomial is 4 So the 1 is multiplied by a power of x which is 1 lower than the degree of the original polynomial One lower than 4 is 3, so we write x 3 after the 1 Then we write x 2 after the first 7 Then x after the second 7 The third 7 on the bottom is the constant term. But, the product of zeroes in any quadratic polynomial equation is given by = constant term / coeffof t 2 = −15/1 = −15 Hence, the relationship is verified (vi) 3x2 – x – 4 3x2 − x − 4 = 3x2 – 4x 3x − 4 = x (3x – 4) 1(3x – 4) = ( x 1) (3x – 4) ∴ zeroes of the given polynomial are – {−1, 4/3 }. Factoring polynomials We have seen above that when we study a polynomial, we need to specify what kind of solutions/factors we are looking for In particular, suppose p (x) is a polynomial with degree greater than 0, and real coefficients, over the comple x numbers p (x) factors into linear factors.
(vi) 3x2 – x – 4 Let p(x) = 3x2 – x – 4 Zero of the polynomial is the value of x where p(x) = 0 Putting p(x) = 0 3x2 x – 4 = 0 We find roots using splitting the middle term method ⇒ 3x2 – 4x 3x – 4 = 0 ⇒ x(3x – 4) 1(3x 4) = 0 ⇒ (3x – 4)(x 1) = 0 So x = 4/3 , x = – 1 Therefore, α = 4/3 & β = – 1 are the. Question 7 of 21 Factor the polynomial 3x2(x 4) 5(x 4) O A 3x2(x – 4) O B (x4)(3x2 5) O C (x4)(3x2 5) O D (x 4)(3x – 5) Answers 2 Get Other questions on the subject Mathematics Mathematics, 1630, josh Find the quotient 50a2 – 98b2 5a 7b. Answer Save 1 Answer Relevance Dee W Lv 7 1 decade ago Favorite Answer 6x^3 15x^2 2x^2 5x 8x = 6x^3 13x^2 13x 1 0 Still have questions?.
See a solution process below Because the x^4 coefficient is 1 we know the coefficient for the x^2 terms in the factor will also be 1 (x^2 )(x^2 ) Because the constant is a negative and the coefficient for the x term is a negative we know the sign for the constants in the factors will have one positive and one negative (x^2 )(x^2 ) Now we need to determine the factors which multiply to. X 2 – x. By Factor theorem, xk is a factor of the polynomial for each root k Divide x^{3}3x^{2}4 by x1 to get x^{2}4x4 Solve the equation where the result equals to 0.
Polynomial Long Division Calculator The calculator will perform the long division of polynomials, with steps shown Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x` In general, you can skip parentheses, but be very careful e^3x is `e^3x`, and e^(3x) is `e^(3x)`. Subtracting polynomials works almost exactly the same way as does adding polynomials This lesson demonstrates both vertical and horizontal subtraction of polynomials, and demonstrates how to keep track of those "minus" signs. If the polynomial x 4 – 6x 3 16x 2 – 25x 10 is divided by another polynomial x 2 – 2x k, the remainder comes out to be (x α ), find k and α Sol Applying the division algorithm to the polynomials x 4 – 6x 3 16x 2 – 25x 10 and x 2 – 2x k, we have.
Hence, the required quadratic polynomial is 4x2 x 4 (ii) Let α and β are the zeroes of the quadratic polynomial ax2 bx c Given, α β = √2= 3√2/3 = b/a and α * β = 1/3 = c/a On comparing, we get a = 3, b = 3√2, c = 1 Hence, the required quadratic polynomial is 3x2 3√2x 1. Divide first polynomial by second polynomial and write the answer in the form ‘Dividend = Divisor × Quotient Remainder’ i x 3 – 64;. Use factoring to find zeros of polynomial functions Find zeros of polynomial functions Recall that if f is a polynomial function, the values of x for which latexf\left(x\right)=0/latex are called zeros of fIf the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros.
1 2 3 4 23 Evalute 2x3 3x2 4x 5 with x = 4 100 101 102 103 24 What is the coefficient of the second. Get your answers by asking now Ask Question 100 Join Yahoo Answers and get 100 points today. Question Question 1 Evaluate The Polynomial Function Of P(x) = 3x2 X 4 And Find P(3) P(3) = 7 P(3) = 24 P(3) = 26 P(3) = 28 05 Points Question 2 A Wooden Plank Is (2x2 5x 9) Meters Long If A Piece (x2 5) Meters In Length Is Cut Off The Plank, How Long Is The Remaining Piece?.
There are a few rules as to what polynomials cannot contain Polynomials cannot contain division by a variable For example, 2y 2 7x/4 is a polynomial, because 4 is not a variable However, 2y27x/(1x) is not a polynomial as it contains division by a variable Polynomials cannot contain negative exponents You cannot have 2y2 7x4 Negative. There is a polynomial which, when multiplied by x^2 2x 3, gives 2x^5 3x^4 8x^3 8x^2 18x 9 What is that polynomial?. The function is not a polynomial function because the term 2x1 has an exponent that is not a whole number Decide whether the function is a polynomial function If it is, 3x2 — x 4 x2 2x 4 Add the opposite Add the opposite Add the polynomials a 3x3 2x2 —x —7 — 8 4x3 — 8x2 — x 1 b (9x3 — 2x 1) (5x2 12x.
See a solution process below Because the x^4 coefficient is 1 we know the coefficient for the x^2 terms in the factor will also be 1 (x^2 )(x^2 ) Because the constant is a negative and the coefficient for the x term is a negative we know the sign for the constants in the factors will have one positive and one negative (x^2 )(x^2 ) Now we need to determine the factors which multiply to. This gives us 11x. A polynomial equation used to represent a function is called a For example, the equation f(x) 4 2 5 2 is a quadratic polynomial function, and the equation p(x) 2x3 4x2 5x 7 is a cubic polynomial function Other polynomial functions can be defined by the following general rule.
Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Pi (Product) Notation Induction Logical Sets Pre Calculus. Also, polynomials of one variable are easy to graph, as they have smooth and continuous lines Example x 4 −2x 2 x See how nice and smooth the curve is?. We can find this with polynomial division 2x^3 x^2 4x 3 x^2 2x 3 2x^5 3x^4 8x^3 8x^2 18x 9 2x^5 4x^4 6x^3 _____.
Start with the given polynomial Plug in Raise 15 to the second power to get 225 Multiply 3 and 15 to get 45 Now combine like terms So the vertex is (15,625) Here is a graph to see the vertex and yintercept. Simplify polynomial expressions This calculator will simplify polynomials as much as possible show help. Answer Save 1 Answer Relevance Dee W Lv 7 1 decade ago Favorite Answer 6x^3 15x^2 2x^2 5x 8x = 6x^3 13x^2 13x 1 0 Still have questions?.
Question 7 of 21 Factor the polynomial 3x2(x 4) 5(x 4) O A 3x2(x – 4) O B (x4)(3x2 5) O C (x4)(3x2 5) O D (x 4)(3x – 5) Answers 2 Show answers Another question on Mathematics Mathematics, 1600 Hiw many different triangles can be constructed with side measurements 6 centimeters,9centimeters,and 13. Quadratic polynomial can be factored using the transformation ax^{2}bxc=a\left(xx_{1}\right)\left(xx_{2}\right), where x_{1} and x_{2} are the solutions of the quadratic equation ax^{2}bxc=0 Quadratic polynomial can be factored using the transformation a x 2 b x c = a ( x − x 1 ) ( x − x 2 ) , where x 1 and x 2 are the solutions. Get your answers by asking now Ask Question 100 Join Yahoo Answers and get 100 points today.
Polynomial Long Division Calculator The calculator will perform the long division of polynomials, with steps shown Show Instructions In general, you can skip the multiplication sign, so `5x` is equivalent to `5*x` In general, you can skip parentheses, but be very careful e^3x is `e^3x`, and e^(3x) is `e^(3x)`.

Find The Zeroes Of The Following Quadratic Polynomials And Verify The Relationship Between The Zeroes And The Coefficients 3x 2 X 4

On Dividing X3 3x2 X 2 By A Polynomial G X The Quotient And Remainder Were X 4 And 6 Respectively Brainly In
Cbse 10 Math Ncert Solutions

Long Polynomial Division
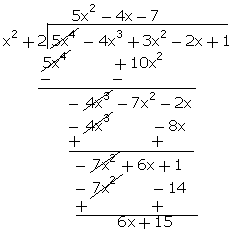
On Dividing The Polynomial P X 5x4 4x3 3x2 2x 1 By Another Polynomial G X X2 2 If The Quotient Is Ax2 Bx C Find A B And C Mathematics Topperlearning Com 3osk2prr

Divide Polynomial X4 2x3 3x2 4x 5 By X 2 Using Synthetic Division Method Andwrite The Brainly In
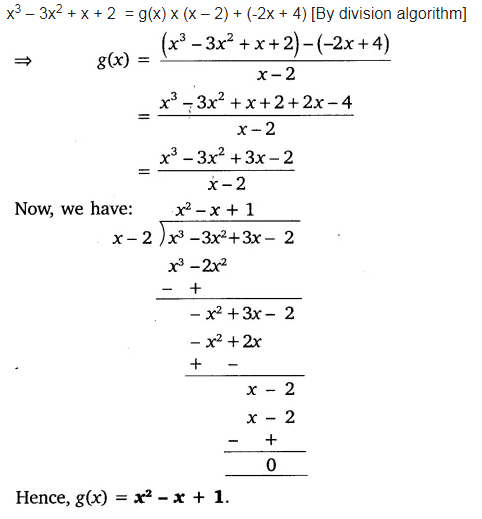
On Dividing X3 3x2 X 2bya Polynomial G X The Quotient And Remainder Were Cbse Class 10 Maths Learn Cbse Forum
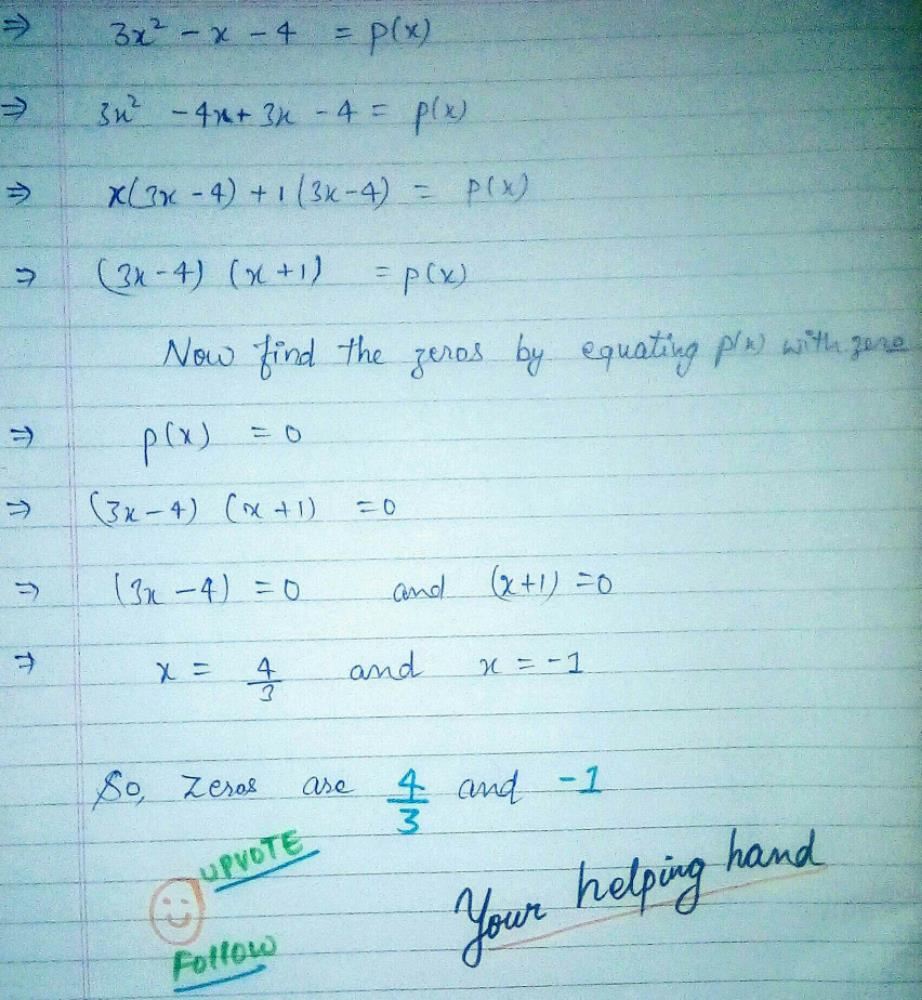
Find The Zeros Of The Following Quadratic For The Equation 3 X Square Minus X Minus 4 Related 03 Relationship Between Zeroes And Coefficient Of Polynomials Edurev Class 10 Question

How To Solve X 4 4 3x 2 And Check Polynomial Inequality Youtube

Ex 2 3 4 On Dividing X3 3x2 X 2 By Polynomial G X

Find The Zeros Of Polynomial 3x2 X 4 Brainly In

On Dividing X 3 3x 2 X 2 By A Polynomial G X The Quotient And Remainder Were X 2 And 2x 4 Respectively Find G X

Find All The Zeroes Of The Polynomial 3x 4 6x 3 2x 2 10x 5 Myaptitude In

Find The Zeros Of The Quadratic Polynomial 3xsquare X 4 And Verify The Relationship Between The Brainly In

The Product Of Two Zeroes Of Polynomial P X X 3 3x 2 6x 8 Is 2 Find All

Ex 2 2 1 Class 10 Find Zeroes Of Quadratic Polynomials And Verify

Solved Question 7 Factor The Polynomial By Grouping If P Chegg Com

Answered Use The Intermediate Value Theorem To Bartleby
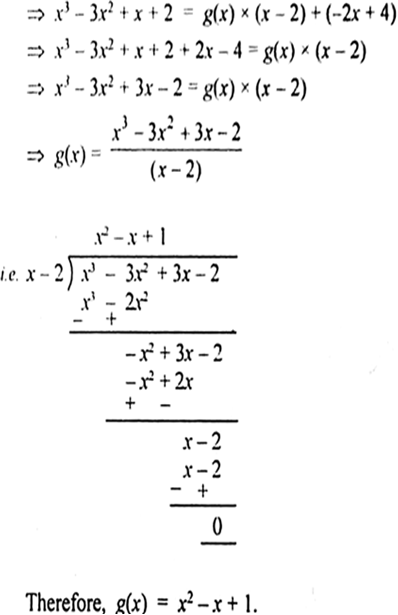
Find The Zeroes Of The Quadratic Polynomial X2 5x 6 And Verify The Relationship Between The Zeroes And The Coefficients From Mathematics Polynomials Class 10 Punjab Board

Answered A Classify The Following Polynomials Bartleby

The Polynomial F X X 4 2x 3 3x 2 Ax B

Ex 2 4 3 Optional If Zeroes Of Polynomial X3 3x2 X 1 Are A

Algebra Teacher S Activities Kit 150 Activities That Support Algebra In The Common Core Math Standards Grades 6 12 Pdfdrive Com Flip Book Pages 151 0 Pubhtml5

How To Factorise X 4 3x 2 Quora

Polynomials Exercise 2 3 Class 10 Breath Math
The Polynomial P X X4 2x3 3x2 Ax 3a 7 When Divided By X 1 Leaves The Remainder 19 Studyrankersonline
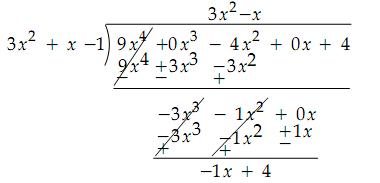
On Dividing The Polynomial P X 9x4 4x2 4 By The Polynomial G X 3x2 X 1 The Remainder Is Ax B Find A And B Mathematics Topperlearning Com Ab5z94lss

Polynomial Functions

Write Factors Of 3x2 X 4 Math Polynomials Meritnation Com

Module 1 Polynomial Functions
Obtain All Zeros Of The Polynomial X X 4 3x 2 X 2 9x 6 If Two Of Its Zeros Are 3 And 3 Sarthaks Econnect Largest Online Education Community

Polynomials

Q On Dividing X3 3 X2 X 2 By A Polynomial G X Math Polynomials Meritnation Com

Solve This Q 1 Divide Fx 9x4 4x2 4 By Gx 3x2 X 1 Find The G X R X Math Polynomials Meritnation Com

Module 1 Polynomial Functions

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

13 Find All Zeroes Of 2x 4 3x 3 3x 2 6x 2 If You Know That Two Of Its Zeroes Are S Youtube

Module 1 Polynomial Functions
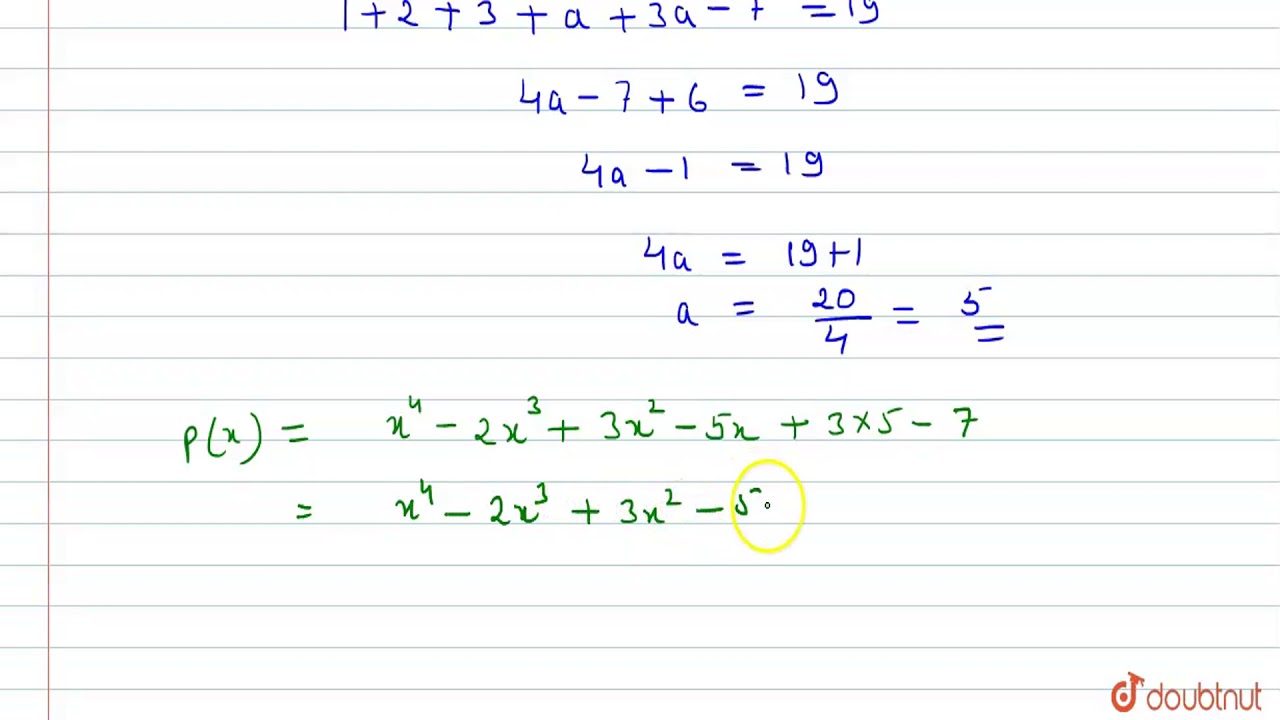
The Polynomial P X X 4 2x 3 3x 2 Ax 3a 7 When Divided By X 1 Leaves The Remainder 19 Youtube
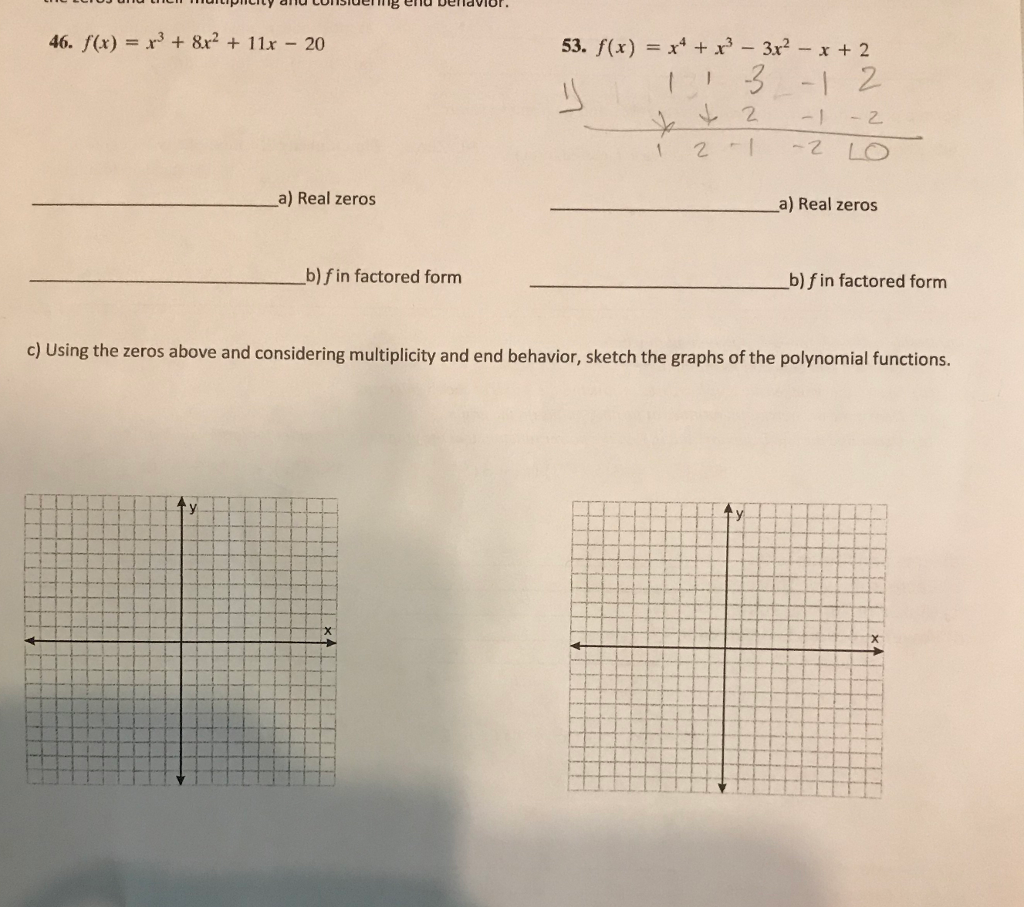
Solved 46 F X X3 8x2 11x 53 F X X4 3 3x2 X Chegg Com
View Question Just A Few Questions

G 1 Coaching Class 2nd Chapter Polynomials

Module 1 Polynomial Functions
Polynomials Algebra 2

Find The Zeroes Of The Following Quadratic Polynomials And V Scholr

Find Zeroes Of Quadratic Polynomial 3x 2 X 4 Polynomials Class 10 Mathematics Youtube

Polynomial Functions
Find The Zeros Of The Polynomial F X 4 3x 5x 2 3 Verify The Relationship Between The Zeros Its Coefficients Quora

Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes

Solved Hsa Apr A Multiplying Polynomials Co 2e3 Multiply Chegg Com

1 Simplify 2 9a B Answer 18a 2b 2 Simplify R2s Rs3 Answer Ppt Download
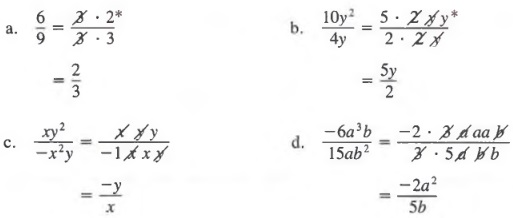
Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver
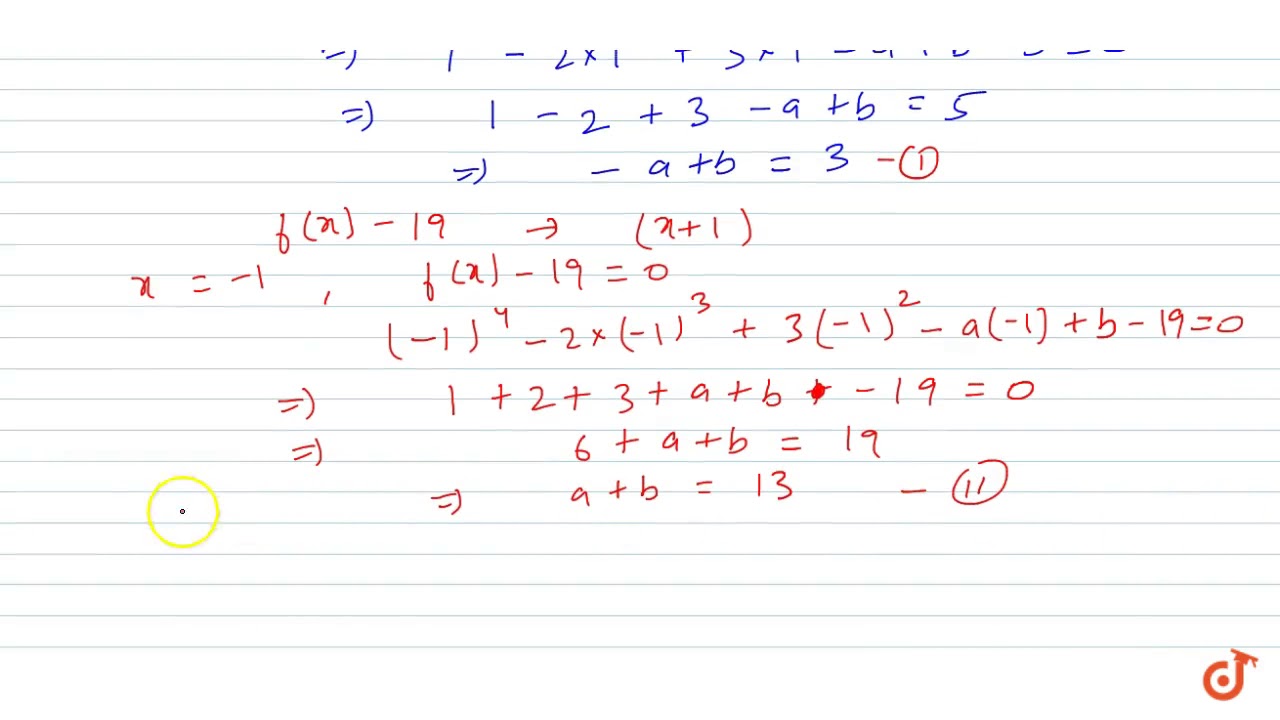
The Polynomials F X X 4 2x 3 3x 2 Ax B When Divided By X 1 And X 1 Leaves The Youtube

Solved For The Polynomial Function F X X4 2x3 3x2 4x Chegg Com

Solving Polynomials Ppt Download

On Dividing X 3 3x 2 X 2 By A Polynomials G X The Quotient And Remainder Were X 2 And 2x 4 Respectively Find G X

Divide And Write The Quotient And The Remainder 3x 2x2 4x3 X 4 Mathematics Shaalaa Com

B Find The Zeroes Of Quadratic Polynomial F X 3x2 X 4 Scholr

Rd Sharma Class 9 Solutions Maths Chapter 6 Factorization Of Polynomials

Liiduumber 10 Find The Zeroes Of The Quadratic Polynomial 3y2 V O
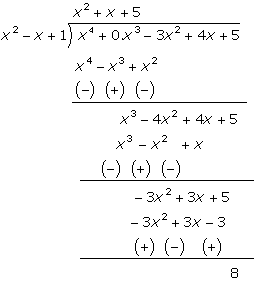
Divide X4 3x2 4x 5 By X2 X 1 And Verify That Dividend Divisor Quotient Reminder Mathematics Topperlearning Com 6zrz1vqq
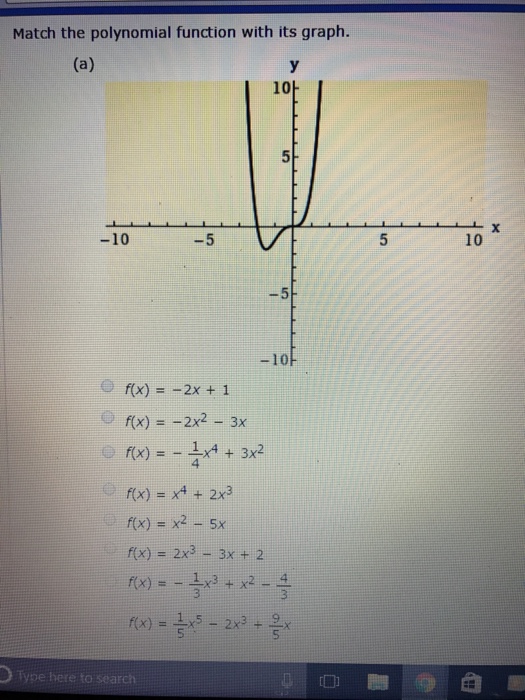
Solved Match The Polynomial Function With Its Graph F X Chegg Com

Find That 3x 2 X 4 Maths Questions

Check Whether 2x 4 3x 3 3x 2 6x 2 Is Divisible By X 2 2

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 4 Polynomials

What Must Be Added To F X 6x5 5x4 11x3 3x2 X 5 So That It May Be Exactly Divisible By G X 3x2 2x 4 Mathematics Topperlearning Com 6ocvt9cnn

Algebraic Long Division An Introduction Dividing Polynominals

Iv 40un Vi 3x2 X 4adratic Polynomial Each With The Given Numb
Find The Zeros Of The Polynomial F X 4 3x 5x 2 3 Verify The Relationship Between The Zeros Its Coefficients Quora

Ex 2 2 1 Class 10 Find Zeroes Of Quadratic Polynomials And Verify
Find The Zeroes Of The Quadratic Polynomials 3x 2 X 4 And Verify The Relationship Between The Zeroes And The Coefficients Sarthaks Econnect Largest Online Education Community

Find The Zeroes Of The Quadratic Polynomial 3x2 X 4 And Verify The Relationship Between The Zeroes And Brainly In

Factorise 3x2 X 4 Factorise 3x 2 X 4 Youtube
Find The Zeros Of The Polynomial F X 4 3x 5x 2 3 Verify The Relationship Between The Zeros Its Coefficients Quora

A Controllable Graph On Eight Vertices Having Characteristic Polynomial Download Scientific Diagram
How Do You Find The Quotient Of 3x 2 2x 4 By X 3 Socratic

Advanced Level Mathematics Pure Mathematics 2 3 By Cambridge University Press Education Issuu

Solve For X In This Complex Equation X 4 3x 2 4 0 Youtube
Solved Consider The Polynomial Function F X X4 3x3 3x2 Whose Domain Is Co Co A Find The Intervals On Which F Is Increasing Enter Y Course Hero

Exercise 2 2find The Zeroes Of The Following Quadratic Polynomials

If F X X 4 2x 3 3x 2 Ax B Is A Polynomial Such That When It Is Divided By X 1 And X 1 Then Remainders Are
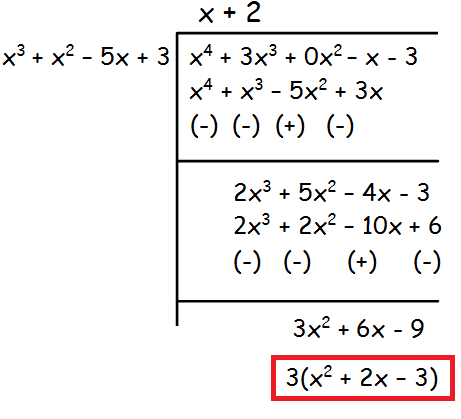
Gcd Of Polynomials Using Division Algorithm
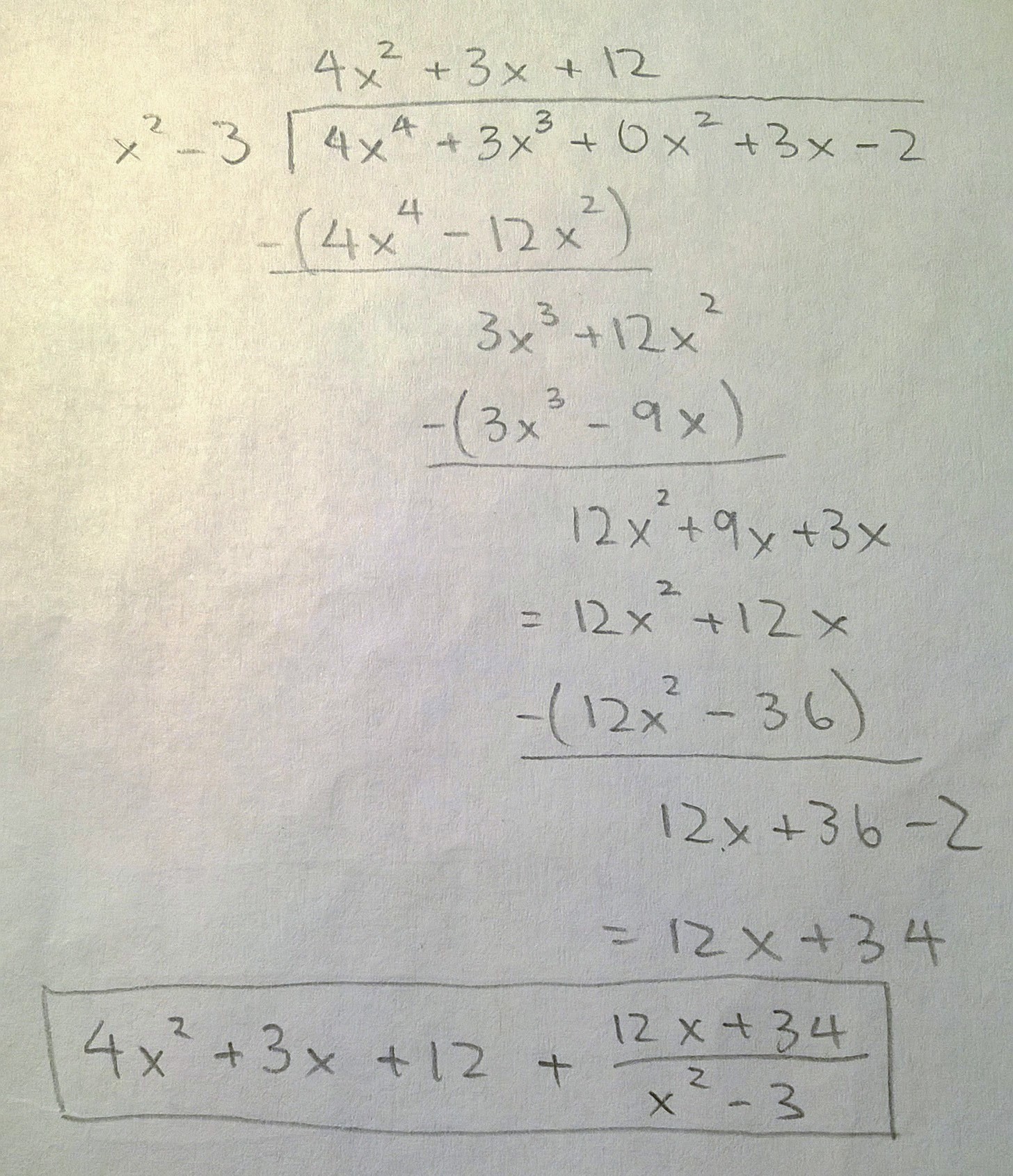
How Do You Divide 4x 4 3x 3 3x 2 X 2 3 Using Polynomial Long Division Socratic



